本当に結構高頻度で数学偏差値50以下だったのによくエンジニアになったものです。(まぁそんなに業務で数学使わないっていうのはあるけど)
常々ソフトウェアエンジニアに向いていないと感じながら問題を解いています。
もとのリンクはこちら。
https://leetcode.com/problems/maximum-value-at-a-given-index-in-a-bounded-array/description/
You are given three positive integers: n, index, and maxSum. You want to construct an array nums (0-indexed) that satisfies the following conditions:
nums.length == n
nums[i] is a positive integer where 0 <= i < n.
abs(nums[i] – nums[i+1]) <= 1 where 0 <= i < n-1. The sum of all the elements of nums does not exceed maxSum. nums[index] is maximized. Return nums[index] of the constructed array. Note that abs(x) equals x if x >= 0, and -x otherwise.Input: n = 4, index = 2, maxSum = 6
Output: 2
Explanation: nums = [1,2,2,1] is one array that satisfies all the conditions.
There are no arrays that satisfy all the conditions and have nums[2] == 3, so 2 is the maximum nums[2].
つまり、Input: n = 4, index = 2, maxSum = 6
がきた場合、配列の長さは4、値を最大にしたいindexは2、配列の合計は6までとなります。
例にもあるようにこの場合は[1,2,2,1]がサイズ4のArrayとして最大でとりうる値。
制約通り、配列の中で隣接する値の差分は絶対値で0から1まで。つまり[1,2,5,1]とかはだめ。
nums[i]は0 <= i < nとは書いてあるけどpositive integerに0は含まないのでArrayの各値のとりうる最小値は1になります。
解き方
大きく分けると2つのパートに分けることができます。
2:Binary searchでmaxSumを超えない、かつindexを最大にする数を探す
2に関しては、Binary searchに慣れている人であれば問題はないでしょう。
厄介なのは1の部分ですね。
問題をわかりやすくするために、
例えばInput: n = 8, index = 4, maxSum = 10というインプットが来たと仮定しましょう。
この場合、index:4の値を最大にしつつ、合計は10以下にしなければなりません。
たとえば最初は適当にindex4に8をいれます。そうすると制約上index4を起点に左側の
index 3は7
index 2は6
という感じで取れる値が決まっていきます。右側も同様に値をとって図のようになります。
ただ、合計は当然ながらこの配列の合計の値はMaxSumの10を超えます。
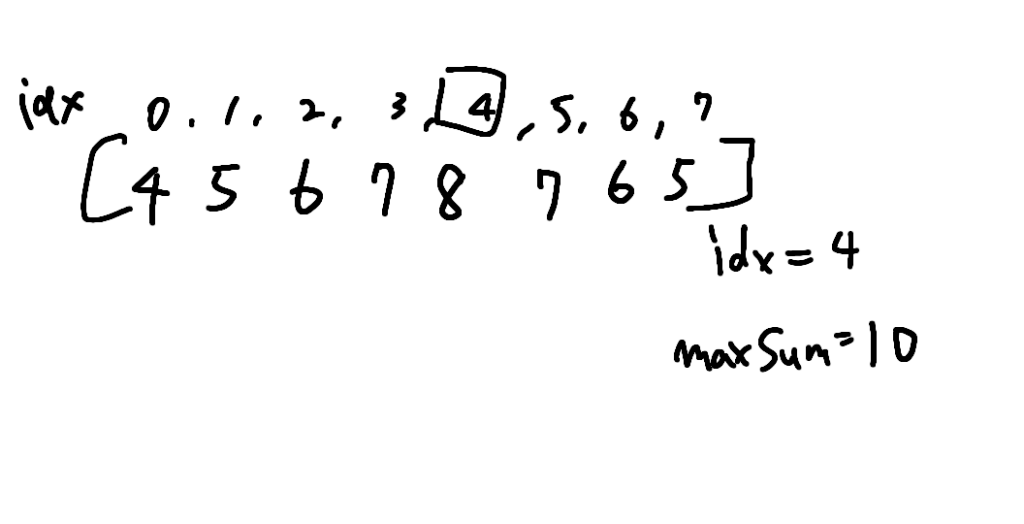
では今度は、例えば仮にindex4に3を置いてみたとします。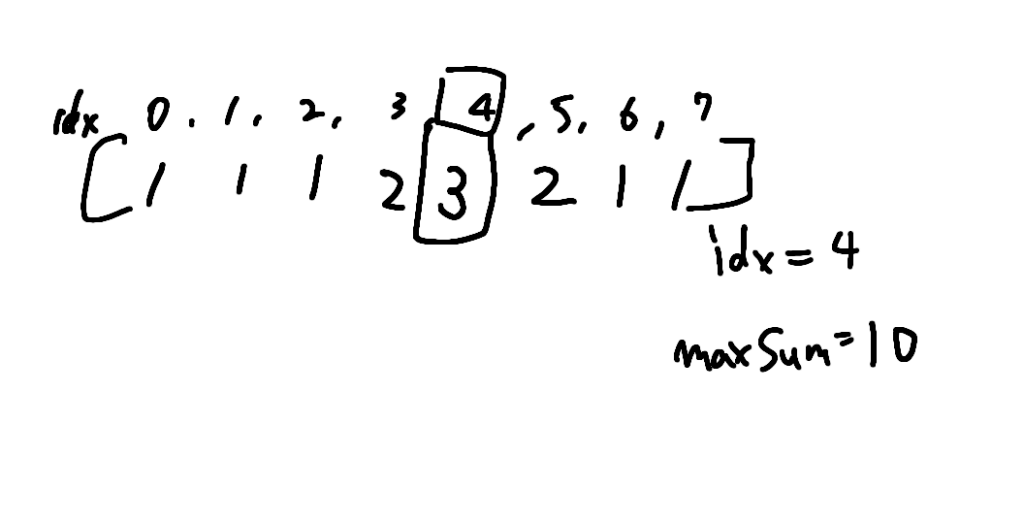
そうするとindex4を起点に左側の
index 3は2
index 2は1
それ以降は1の値をとる
という感じで取れる値が決まっていきます。右側も同様に値をとって上の図のようになります。
ただこの場合も配列の全ての値の合計は12になるので、これは回答にならないケースです。
さらにindexの値をさげる必要があります。
こんなふうに、index4におくべき適切な値を、sumの値を計算しながら模索していくしかないというのがこの問題のLovelyなところでしょう。
ではindex 4にどんな値をいれて検証していけばいいか、というのは後で考えるとして、
毎度毎度Sumの計算はどうしたらいいのでしょうか。
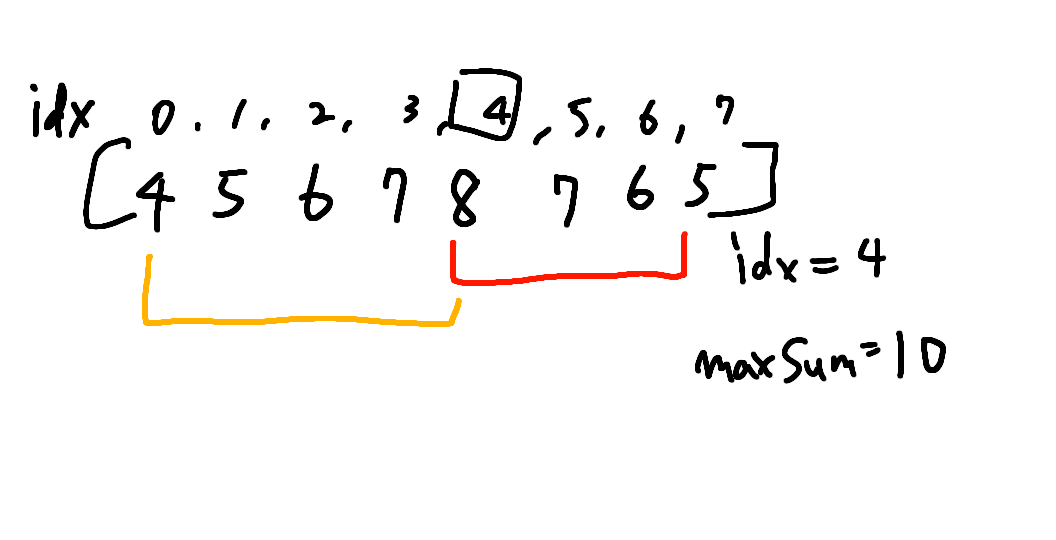
まずはこのindex 4に8を置いてみたパターンから考えます。
index4を起点として、左のオレンジと右の赤の部分について別々について考えます。
まずはオレンジから。4,5,6,7,8の合計を考えます。普通に計算してもいいですが、
隣接する値の差分が1であることから、等差数列(でた!!!文系564!)で計算できます。
等差数列ってなんだよっていう人は一回このYoutubeをみてきてください。(気持ちはわかるよ、もう逃げたいよな)
細かいことは抜きにすると、等差数列だったら(最初の値 + 最後の値) * 値の個数 / 2で合計が計算できちゃうよってこと。4,5,6,7,8を計算するにあたって、
(最初の値 + 最後の値) * 値の個数 / 2に当てはめて考えましょう。
最初の値4はvalue (最初index4にいれた適当な値8のこと) – 4(index)
最後の値はvalue
値の個数はindex + 1ですね。
つまりオレンジの箇所は(value – index + value) * (index+ 1) /2となります。
では赤の箇所はどう計算できるでしょうか。(8,7,6,5の合計)
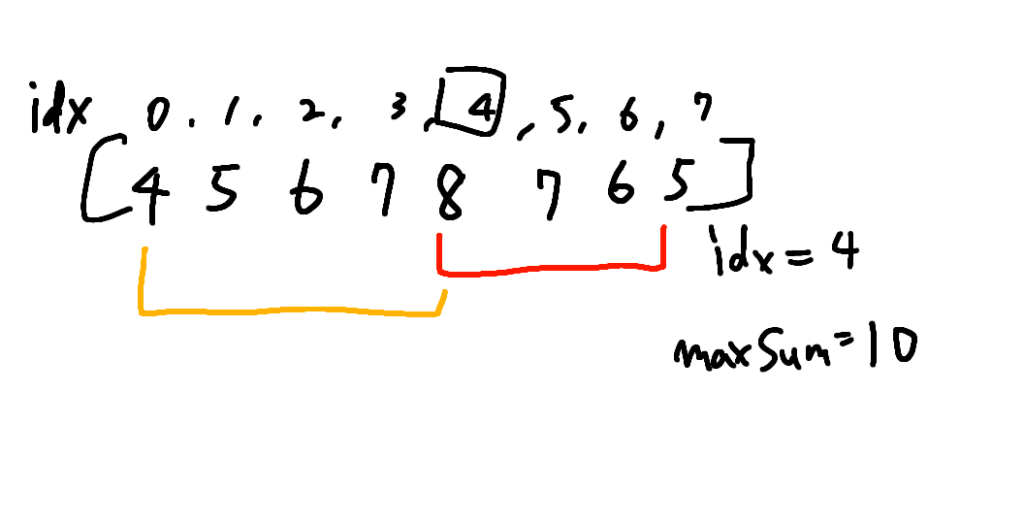
同じように等差数列なので、(最初の値 + 最後の値) * 値の個数 / 2に当てはめて考えます。
最初の値はvalue
最後の値は5なのですが、これはvalue から (n – 1) – (index)
=> indexの7-4間の距離をvalueから引きます。なぜならindex 4-7分だけ8から-1されるからです。
つまりvalue – (n-1-index) => value – n +1 + indexとなります。
値の個数は(n-1) – index + 1(個数を数える場合は+1) => n-indexですね。
つまり赤の箇所は(value + value – n + 1 + index) * (n – index) / 2となります。
また、オレンジになる時の条件はvalue(index4に適当に置いた数)がvalue > index のとき
赤になるときの条件はvalue > n – index ( 8,7,6,5 と減らしたときにindexからnまでの長さが十分にある= 連続する1,1,1,1,の値を生まないとき)となります。
あーもうしんどいですね、文系的にはもうしんどいですね、わかります。
では次はこのパターンを見ていきましょう。
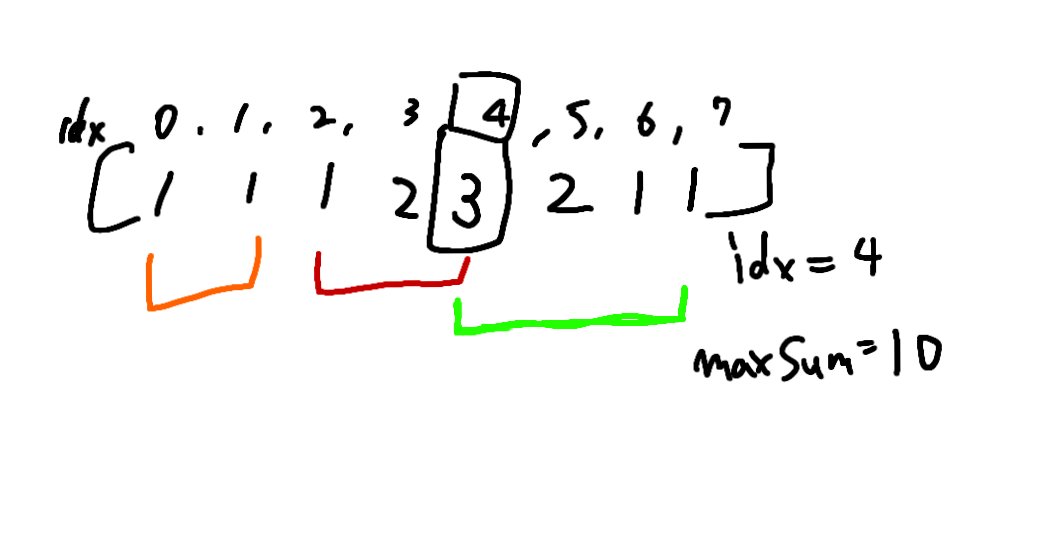
index 4を起点として左側は、等差数列+1の羅列となっています。
この状況はvalue(index4に適当に置いた数、ここでいうと3)がindexの値以下のときに起こります。
さて、左側をどう計算するのかというと、
赤の部分は先ほどの等差数列、オレンジの場合は1で埋まっているので長さの計算がそのまま合計になります。
赤の等差数列の場合
(最初の値 + 最後の値) * 値の個数 / 2
なので(1 + value )* 3 / 2となります。
オレンジの部分はvalueがindex以下という前提なのでindex – value + 1(差分プラス1)で計算できます。
では黄緑の部分はどうでしょうか。これもある3,2,1までは等差数列です。
(最初の値 + 最後の値) * 値の個数 / 2に当てはめると、
(value + 1 )* value /2
1が連続する部分(図の例では3,2,1以降の1は連続してないけど)は
(n – 1) – (index) + 1 – value => n – index – value となります。
大体出揃いましたね。 あとはバイナリサーチで適宜index ( 今回の例ではindex4)に当てはまる数字をいれていって計算します。(解説しようとおもったけど力尽きるやつ)
コードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
class Solution { public int maxValue(int n, int index, int maxSum) { int left = 1, right = maxSum; while(left < right){ int mid = (left + right +1) /2; if(getSum(index, mid, n) <= maxSum){ left = mid; }else{ right = mid -1; } } return left; } private long getSum(int index, int value, int n){ long count = 0; //left side calcuration. if (value > index){ count += (long)(value + value - index) * (index +1 )/2; }else{ count += (long)(1 + value )* value /2 + index - value +1; } //right side calcuration. if (value >= n- index){ // compare length if it cause count += (long)( value + value - n + 1 + index)* (n- index)/2; }else{ count += (long)(1 + value )* value /2 + n- index - value; } return count - value; } } |




